どうしてなのかな
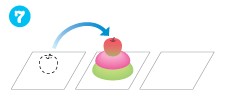
お正月に飾る鏡もち(Newtonなのでリンゴをのせてみました)で数学ゲームに挑戦しましょう。3枚の紙を並べ、そのうちの1枚に鏡もちを置きます。これを、「1回でひとつしか移動させない」、「小さいものの上に大きいものをのせない」という条件を守りながら、ほかの紙の上へ移動させてみましょう。何回の移動でできるでしょう?
そうかなるほど
3段の場合の最少移動回数は7回です。このゲームはフランスの数学者エドワルド・リュカという人が1883年に考え出したもので、「ハノイの塔」と呼ばれています。最少移動回数には法則性があって、数式で表すと(2n-1)となり、3段なら(23-1)=(2×2×2-1)で7回となります。段数と最少移動回数の関係は下の表のようになります。
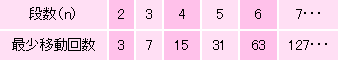
ちなみに、25段に挑戦すると33,554,431回。1回の移動を1秒として、今年のお正月にはじめたゲームが来年のお正月までかかる計算になります。
「ハノイの塔」は身近にあるものを使って楽しめる数学ゲームです。

画用紙の工作例
道具を手づくりするのも楽しいですよ。
![]()
[ルールをもう一度確認しましょう。]
・置ける場所は3カ所だけ
・1回にひとつしか移動させてはいけない
・小さいものの上に大きいものをのせてはいけない
【3段の場合】
3段を7回で移動できましたか?
移動の手順は次のとおりです。
-
1
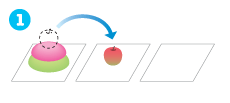
-
2
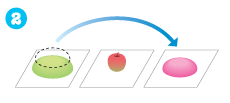
-
3
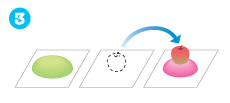
-
4
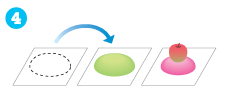
-
5
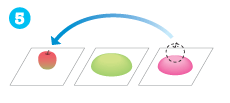
-
6
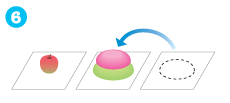
-
7
さらにチャレンジ!
意外にカンタン、もの足りないという人は、段数を増やしてみましょう。
![]()
[ルールをもう一度確認しましょう。]
・置ける場所は3カ所だけ
・2回にひとつしか移動させてはいけない
・小さいものの上に大きいものをのせてはいけない
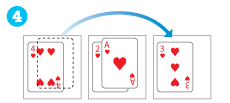
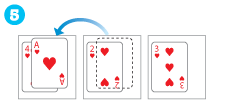
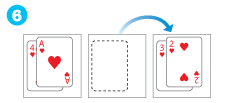
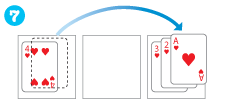
【4段の場合】
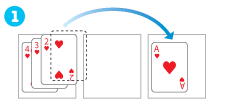
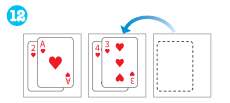
トランプを使うときは、「小さい数字のカードの上に大きい数字のカードをのせない」ということにします。
-
1
-
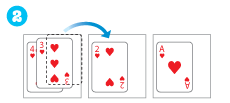
2
-
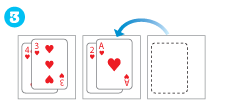
3
-
4
-
5
-
6
-
7
-
8
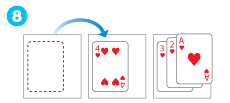
-
9
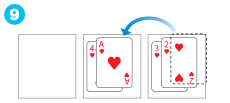
-
10
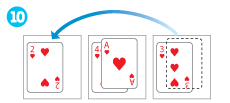
-
11
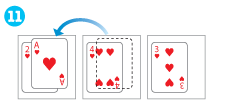
-
12
-
13
-
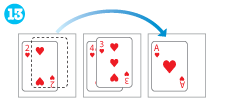
14
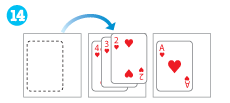
さらにチャレンジ!
意外にカンタン、もの足りないという人は、段数を増やしてみましょう。
トランプなら13段までできますが、最少移動回数は8,191回になります。
NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものです。工作の完成品は市販品と同等ではなく、代用品にもならないことを理解したうえで、個人の責任において実験を行ってください。
NGKサイエンスサイトは日本ガイシが運営しています。ご利用に当たっては、日本ガイシの「プライバシーポリシー」と「ご利用条件•ご注意」をご覧ください。
本サイトのコンテンツ利用に関しては、本サイトお問い合わせ先までご相談ください。





