どうしてなのかな
ピンにまっすぐ当たったビー玉が、右へ行くか左へ行くかの確率は2分の1です。ビー玉がさらに2段目、3段目のピンに当たった場合の確率も、それぞれ2分の1です。では、ビー玉が3つのピンに当たってすべて左側を通る確率はどれくらいでしょうか? 今回は確率を目で見る実験です。写真のような道具をつくって次々にビー玉を落とすと、ビー玉はまん中が高く、外側が低い山のようなかたちになって枠にたまります。こうした確率という考え方を数学的にあつかう基礎をつくったのが、フランスの数学者パスカルです。
そうかなるほど
頂点を「1」としてななめ上の2つの数を加えた値が下にくるような数列をつくると三角形ができます。これを「パスカルの三角形」といい、並んだ数列にはおもしろい性質があります。この三角形を使ってビー玉が落ちてくる確率を計算してみましょう。一番上のピンに当たったビー玉は半分の確率で左右のどちらかを通ります。2段目のピンに当たったビー玉も半分の確率で左右のどちらかを通りますから確率は半分の半分、つまり4分の1になります。ただし、2本のピンの間を通る確率は、左右両方向からビー玉が落ちてくる可能性があるので4分の2となります。このように3段目、4段目と計算をくり返すとビー玉のゆくえの確率がわかります。図のように6段に並んだピンに64個のビー玉を落とした場合、中央の枠には20個のビー玉が集まることになります。実際には寸法の誤差などで数字通りにはなりませんが、全体ではまん中にたくさん集まり、外側の方が少なくなります。つまり、ビー玉はおよそ確率の計算にしたがって落ちているのです。

1. スチレンボード 2枚
(A2サイズ/タテ59.4cm×ヨコ42cm×厚さ0.5cm)
2. プッシュピン 52本)
(右図のような形のもの)
3. ビー玉 60個
(直径1.5cm~1.6cm)
4. 方眼紙 1枚
(B3サイズ/タテ51.5cm×ヨコ36.4cm)
5. カッターナイフ
6. 0.5cm幅両面テープ
7. 定規
8. 鉛筆

![]()
[工作の注意]
・NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものであり、工作の完成品は市販品と同等、もしくは代用品となるものではないことを理解したうえで、個人の責任において実験を行ってください。
・工作・実験を行う際は、必ず手順を読んでから行ってください。
・刃物や器具の取り扱いには十分に注意をし、ケガをしないようにしましょう。
・小学生など低年齢の方が工作を行う場合は、必ず保護者と一緒に行ってください。
-
1
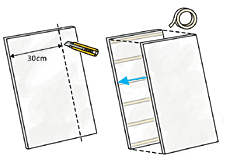
スチレンボード2枚を30cm幅に切り、両面テープではり合わせます。
-
2
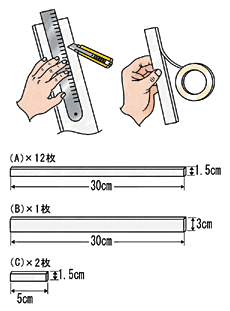
余ったスチレンボードから(A)、(B)、(C)を切り、片方の切断面に両面テープをはります。
-
3
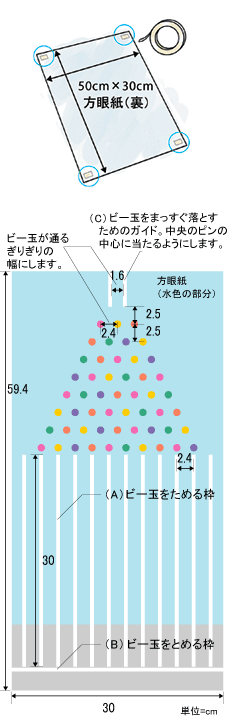
方眼紙をタテ50cm×ヨコ30cmに切り、両面テープでスチレンボードの上にはります。そして図のように、2.4cm間隔(ビー玉がギリギリ通る幅)に正確にピンをさし、部品をはりつけます。
![]()
[実験の注意]
・NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものであり、工作の完成品は市販品と同等、もしくは代用品となるものではないことを理解したうえで、個人の責任において実験を行ってください。
・工作・実験を行う際は、必ず手順を読んでから行ってください。
・刃物や器具の取り扱いには十分に注意をし、ケガをしないようにしましょう。
・小学生など低年齢の方が工作を行う場合は、必ず保護者と一緒に行ってください。
-
1
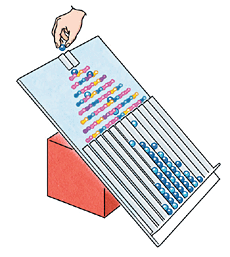
台をおよそ45度の角度に立てかけ、ガイドからビー玉を落とします。ビー玉のたまり方は中央部に多く外側の方ほど少なくなります。
-
2

ピンが8段並んだ台に60個のビー玉を落とすと、まん中の枠には・・・
60×256分の70
つまり16~17個のビー玉がたまる計算になります。繰り返し60個のビー玉を落としてみましょう。結果はほぼ同じになります。
NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものです。工作の完成品は市販品と同等ではなく、代用品にもならないことを理解したうえで、個人の責任において実験を行ってください。
NGKサイエンスサイトは日本ガイシが運営しています。ご利用に当たっては、日本ガイシの「プライバシーポリシー」と「ご利用条件•ご注意」をご覧ください。
本サイトのコンテンツ利用に関しては、本サイトお問い合わせ先までご相談ください。





