どうしてなのかな
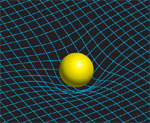
陣笠のようにした紙をひっくり返してビー玉をころがすと、だ円軌道をえがいて動きます。中心近くではスピードが速くなり、中心から離れるとゆっくりころがって、なかなか穴に落ちません。ついみとれてしまいますね。太陽をまわっている惑星も、同じような動きをしているんですよ。
そうかなるほど
ケプラーは惑星の動きを3つの経験的な法則にまとめました。ニュートンはケプラーの法則などから、物質には互いに引きあうという性質があり、2つの物体の間には質量に比例し、距離の2乗に反比例する引力がはたらくという万有引力の法則を発見しました。つまり、惑星の運動とリンゴが木から落ちる現象は同じということですね。そしてアインシュタインは、ちょうどふかふかのふとんに乗るとふとんが沈むように、万有引力(重力)は質量を持つ物質が引きおこす時空のゆがみだという一般相対性理論を考えました。つまり、地球が太陽のまわりをまわるのは、引力によって地球の進行方向が曲げられるのではなく、太陽の質量によってゆがめられた時空に沿って動くことで、地球はだ円軌道をえがいていると考えたのです。
ケプラーの法則
•第1法則:
惑星は太陽をひとつの焦点とするだ円軌道を公転する
•第2法則:
惑星と太陽とを結ぶ線が一定時間にえがく扇形の面積は、惑星が軌道のどこにいても同じになる。つまり、太陽に近いところでは惑星は速度を増し、遠いところでは速度を落とす(面積速度が一定)
•第3法則:
惑星の公転周期の2乗は、だ円軌道の長い方の半径の3乗に比例する。つまり、長い方の半径が同じであれば、だ円軌道がどれだけつぶれていても、また、円軌道であっても公転の周期は同じになる。
材料
1. 厚紙(B2) 1枚
2. ビー玉


工作の完成品
道具
•ひも
•画びょう
•鉛筆
•コンパス
•はさみ
•カッターナイフ
•セロハンテープ
•のり
![]()
[工作の注意]
・NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものであり、工作の完成品は市販品と同等、もしくは代用品となるものではないことを理解したうえで、個人の責任において実験を行ってください。
・工作を行う際は、必ず手順を読んでから行ってください。
・器具の取り扱いには十分注意し、けがをしないようにしましょう。
・小学生など低年齢の方が実験を行う場合は、必ず保護者と一緒に行ってください。
-
1
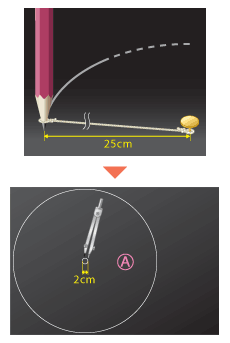
ひもと画びょうをコンパスのかわりにして厚紙に円をかきます。さらにコンパスで円の中心にビー玉が通るくらいの円をかきます。
-
2
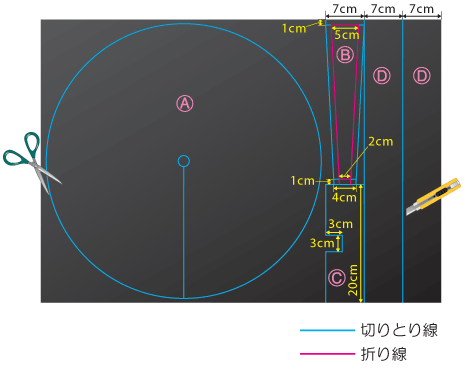
厚紙を図のように切ります。
-
3
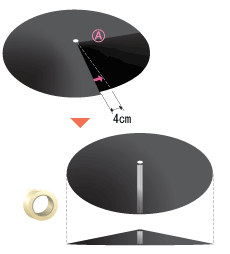
(A)の厚紙を陣笠のようなかたちにし、裏をセロハンテープでとめます。
-
4
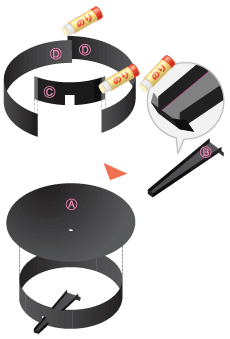
(B)、(C)、(D)を図のように組み立て、(A)と組み合わせます。
![]()
[実験の注意]
・NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものであり、工作の完成品は市販品と同等、もしくは代用品となるものではないことを理解したうえで、個人の責任において実験を行ってください。
・実験を行う際は、必ず手順を読んでから行ってください。
・器具の取り扱いには十分注意し、けがをしないようにしましょう。
・小学生など低年齢の方が実験を行う場合は、必ず保護者と一緒に行ってください。
-
1

ビー玉をころがします。
-
2

ビー玉はだ円をえがきながらころがります。中心近くではスピードが速くなり、中心から離れるとゆっくりころがることがわかります。

ビー玉にりん光スプレーを塗り、暗いところで実験すると、ビー玉の軌跡が観察しやすくなります。
NGKサイエンスサイトで紹介する実験は、あくまでも家庭で手軽にできる科学実験を目的としたものです。工作の完成品は市販品と同等ではなく、代用品にもならないことを理解したうえで、個人の責任において実験を行ってください。
NGKサイエンスサイトは日本ガイシが運営しています。ご利用に当たっては、日本ガイシの「プライバシーポリシー」と「ご利用条件•ご注意」をご覧ください。
本サイトのコンテンツ利用に関しては、本サイトお問い合わせ先までご相談ください。





